こんにちは。関東の大学に通う大学生ミンチ(@programminchi)です。今回は機械学習の学習アルゴリズムである線形回帰について学んでいきましょう。なんだか数式が苦手だなって人も具体例を交えながら説明していくので安心して読み進めてください
機械学習におけるアルゴリズムって何?
アルゴリズムとは一般的に何か問題を解く上での計算方法のことです。
例えば、ある自然数が1つ与えられた時に、それが素数であるかどうか求めたいとします。
1番最初に思いつく方法は恐らく、その自然数よりも小さい2以上の全ての自然数で、与えられた自然数を割って、いずれの自然数でも割り切れなければ与えられた自然数は素数であると判断する手法だと思います。
しかしこの計算方法ではものすごく時間がかかるのでもう少し工夫してみましょう。
与えられた自然数が偶数である時、その自然数は2で割り切れるため、素数ではありません。よって実質、与えられた自然数よりも小さい3以上の奇数で割り切ることができなければ、与えられた自然数は素数であると判断できます。
この方法はすぐに思いつくようなことですが、計算量は最初の方法の半分になっています。
アルゴリズム、つまり問題を解く上での計算方法を少し工夫するだけで大量のデータに対してでも効率の良い計算をしていくことができるのです。
機械学習では大量のデータを扱う必要があるので、このアルゴリズムの選択は非常に重要な課題だといえます。
線形回帰について学ぶ前に

線形回帰について学ぶ前に分類問題と回帰問題について理解しておきましょう。
分類問題と回帰問題
機械学習の教師あり学習には分類問題と回帰問題の2種類があります。
教師あり学習が何か分からない人は以下の記事で詳しく説明しているので参考にしてみてください
分類問題では与えられたデータに対して、そのデータが属するクラスに分けていきます。
例えば、ある動物の画像が与えられた時に、その動物が猫であるか猫でないのか判断するのは分類問題です。これは出力が0か1、つまり離散値で表されるので分類問題であるということができます。
次に回帰問題についてです。これは分類問題とは違って、出力として連続値を得ることを目指しています。
例えば猫の年齢から体重を予想する場合を考えてください。これは体重を予想するわけなので分類問題のように0か1かといった離散値では表現できません。連続値、つまり実数が出力として得られるので回帰問題です。
線形回帰(単回帰)を理解しよう

以下では線形回帰アルゴリズムをできるだけ分かりやすく具体例を挙げながら説明していきます。
線形回帰における仮説関数
まず仮説関数の説明をしていきます。
今6匹の猫がいるとして、それぞれの猫の歳と体重の関係を以下のようにグラフ上にプロットしていきます。
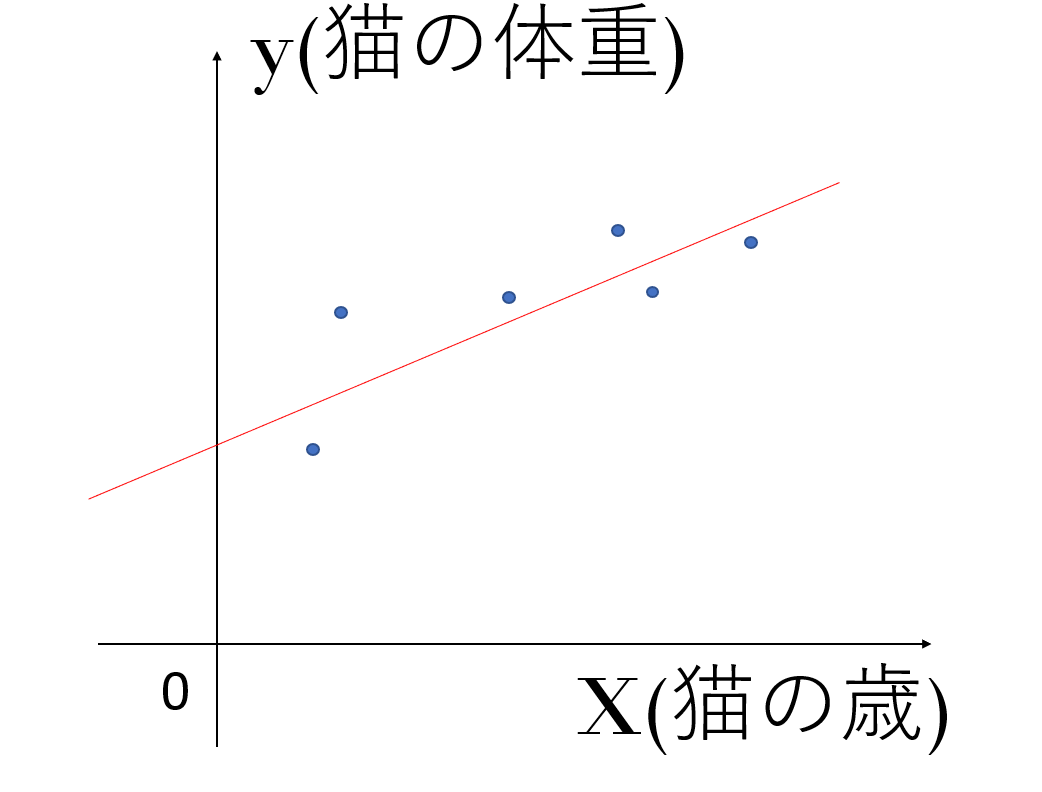
この時、これらのデータを、上の赤色の直線h=ax+bで近似するとします。
このh=ax+bを仮説関数といいます。
そして、この仮説関数を決めると、新たな猫が出てきたとき、その猫の歳からその猫の体重を求めることができます。
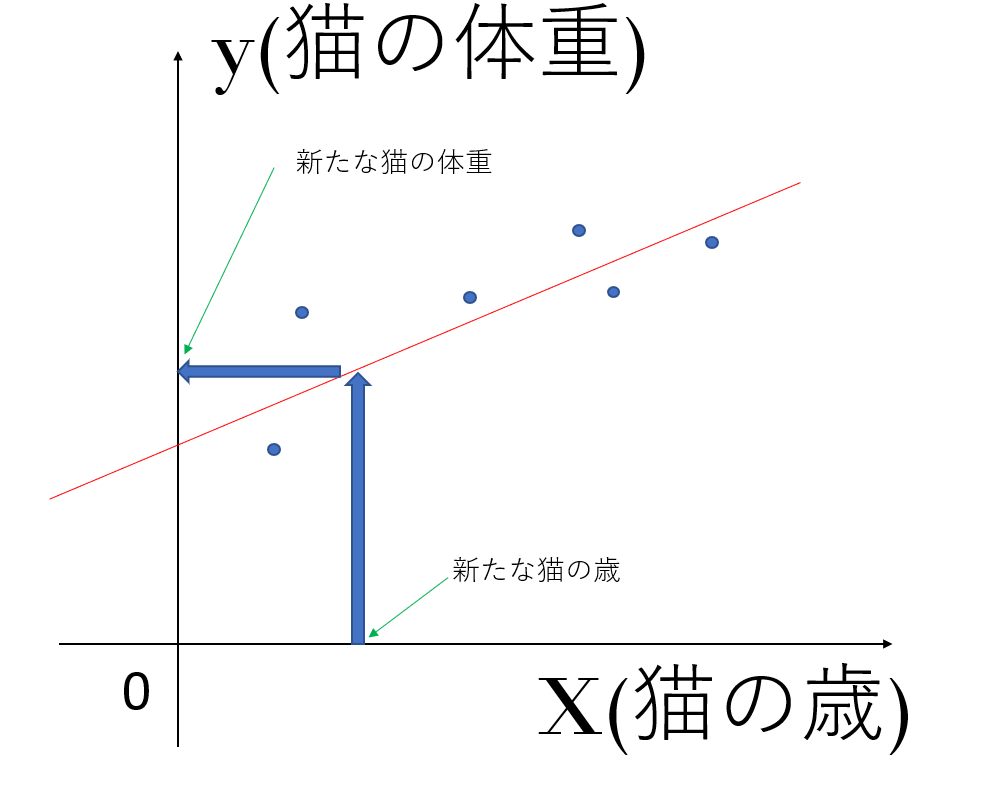
もちろんこの例では、最初に6匹の猫の歳に対するそれぞれの体重(答え)が与えられているので、教師あり学習だと分かると思います。
さらに言うと、入力(新たな猫の歳)に対して出力(新たな猫の体重)が連続値(実数値)として得られているので、これが回帰問題であるということも理解できると思います。
線形回帰における目的関数
仮説関数を定めたことで、入力に対する出力が得られるようになったので、次はどのように仮説関数を求めていくかを説明していきます。
仮説関数を求めるためには目的関数の説明が必要なので以下で詳しく説明していきます。
目的関数を使うと、データに対しどのように最適な直線を当てはめるか算出するのに役に立ちます。
上の例で考えると、6匹の猫のデータは実際には直線上に並んでいませんが、仮に直線で近似しようとしたときに最も全てのデータとの誤差を小さくするような直線を求めるのに役に立つということです。
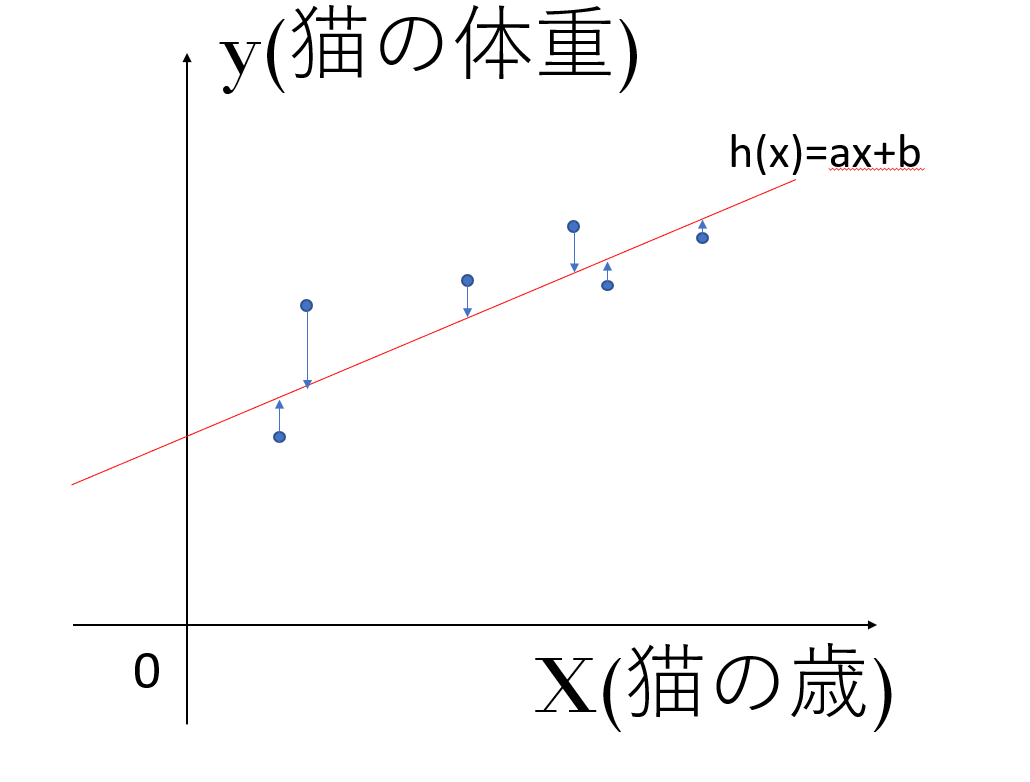
上の図を見てください。青矢印の長さは直線で近似した後の値と、実際のデータの値の間の誤差になります。
今この誤差が小さくなるように直線を決めればよいので、h(x)-yが小さくなるようにしてあげます。ここで、h(x)-yはマイナスになる場合もあるので二乗して考えてあげます。
それではh(x)-yの二乗をそれぞれのデータ(ここでは6匹のデータ)について足し合わせてみましょう。以下の式を見てください。
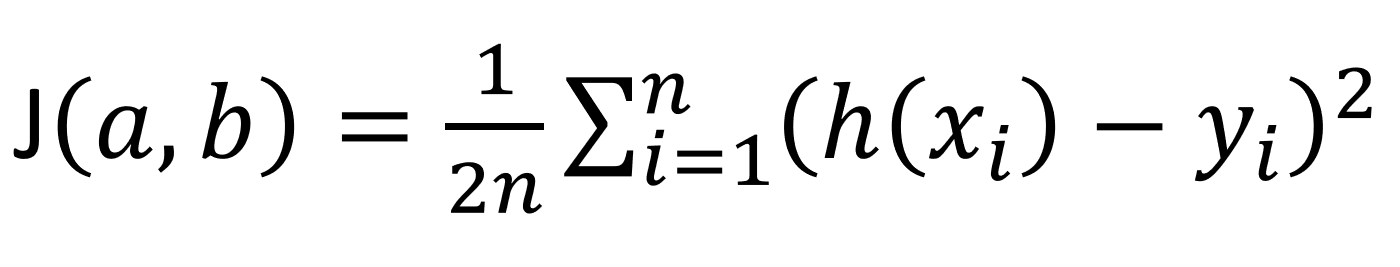
実はこれが目的関数です。
h(x)-yの二乗を全てのデータについて足し合わせているのが分かると思います。上の式ではより一般的なn(匹)という文字で表していますが、分かりづらい人は上のnを6と置き換えて考えてみてください。
また、最初に2nで割っていますが、2で割っているのはこちらの方が計算の都合上やりやすいというのと、nで割っているのはn匹の平均をとるためです。
どちらにせよ深い意味はないので、それぞれのデータについて誤差の二乗を足し合わせて、最後に2nで割ればよいと覚えてください。
目的関数から最適な仮説関数を導く流れ
上では目的関数がどんなものか説明しましたが、この後、どのような流れで仮説関数を導いていくのか説明していきます。
目的関数はそれぞれのデータの誤差を二乗したものの平均であるので、目的関数を最小化すれば、より誤差の小さい直線(仮説関数)が得られるということが直感的に理解できると思います。
よって、目的関数をaとbについて偏微分してあげて、それぞれの偏微分が0になるようなaとbの値が最も誤差の小さい直線を得るための値となります。これによって最適な仮説関数が求められることになります。
まとめ
今回は線形回帰(単回帰)アルゴリズムについて数式を使って理解していきました。
実際に数学的な理解をしていなくてもライブラリを使えば計算はできてしまうことが多いのですが、原理的な部分から理解していくことで機械学習への理解がより一層深まると思うのでじっくり考えてみてください。
今後も定期的にコンピュータ系の記事を発信していくので是非、興味のある人はツイッターの方もフォローお願いします!!