こんにちは。関東の大学に通う大学生ミンチ(@programminchi)です。今回は機械学習の学習アルゴリズムである、ロジスティック回帰について詳しく解説していきます。
機械学習が何か分からない人はまず以下の記事を読んでみてください。
ロジスティック回帰とは?

まずは学習アルゴリズムについて説明していきましょう。
アルゴリズムとは簡単に言うと、問題を解く上での解法です。そしてもちろんこの解法が優れているほど効率よく問題を解くことができます。
機械学習では学習の過程で煩雑な計算をすることが必要になるので、色々な学習アルゴリズムが利用されています。
その学習アルゴリズムの1つがロジスティック回帰です。
ロジスティック回帰を簡単に説明すると、複数の入力を与え、確率yを出力し、その確率からその事象が起こるかどうか分ける2値分類問題です。
天気予報を例に挙げると、雲の様子や、気温、湿度など複数の要素から明日雨が降る確率を予測し、雨が降るのか降らないのか分類するということです。
ロジスティック回帰を直感的に理解しよう

ここからはロジスティック回帰とはどのように分類を行っているのか数式的に見ていきたいと思います。(分かりやすくを意識しているので多少直感的なものになります。)
オッズ比とは?
まずはロジスティック回帰を理解するためにオッズ比という概念から学んでいきましょう。
ここで予測したい事象が起こる確率をpとすると、オッズ比は$\frac{p}{(1-p)}$という風に表されます。この1-pとは予測したい事象が起こらない確率です。
オッズ比はこの式を見れば分かるように、事象の起こりやすさを表すものです。
そしてこのオッズ比に対して対数をとった以下のような式をロジット関数と言います。
$z = \log\frac{p}{(1-p)}$
ここでいう対数とは自然対数のことです。
ロジスティックシグモイド関数
上で述べたロジット関数をzとおき、逆関数を求めると以下のようになります。
$z = \log\frac{p}{(1-p)}$
$exp(z) = \frac{p}{(1-p)}$
$p = \frac{exp(z)}{exp(z) + 1}$
$p = \frac{1}{1 + exp(-z)}$
上で求めた$\frac{1}{1 + exp(-z)}$をロジスティックシグモイド関数、または単にシグモイド関数と言います。
上の式をグラフに描画すると以下のようになります。
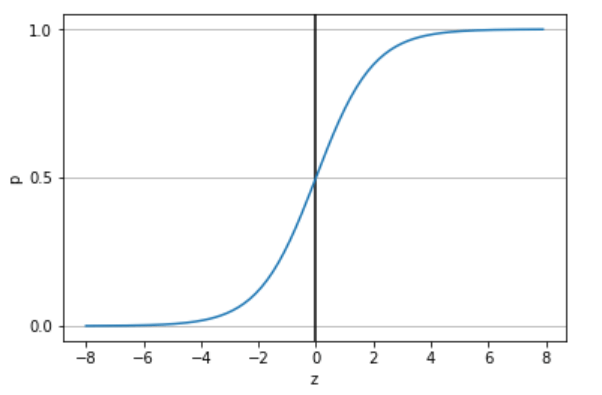
気づいた人もいるとは思いますが、シグモイド関数の出力pは0から1の範囲にあります。つまり、確率が出力されているということです。
そして、ここでzには複数の入力に重みというものを掛け合わせた総和が入ります。(詳しく知りたい人は調べてみてください。)
ロジスティック回帰の分類方法
上ではロジスティックシグモイド関数をグラフに表しました。
出力pが0~1になっており、それを確率ととらえることができるということでしたね。
それではロジスティック回帰アルゴリズムではどこをしきい値として2値分類を行っているのでしょうか。
実は確率pが0.5の点で分類を行っています。
降水確率80%(p=0.8)の時は雨が降ると思う。逆に20%(p=0.2)の時は多分降らないだろうと思う。これと同じことです。
もう一度上と同じグラフを見てください。

これを見ると分かるように、確率pが0.5の点で分類を行うということは、z(ロジット関数)が0の点で分類を行うのと同じことです。
つまりロジスティック回帰アルゴリズムでは、ロジット関数が0より大きいか小さいかで2値分類を行っているのです。
まとめ

今回はロジスティック回帰アルゴリズムについて説明していきました。
正直数学的な話は結構省いているので、直感的な話になってしまいましたが、ざっくりとは理解してもらえたと思います。
少しでも興味がわいたとしたら、もっと詳しく勉強してみてください。
今後も定期的にコンピュータ系の記事を発信していくので是非、興味のある人はツイッターの方もフォローお願いします!!